마름모 넓이 공식 구하는 방법
마름모는 초등부터 고등 수학까지 반복적으로 등장하는 기본 도형이지만, 넓이 공식의 의미와 유도 과정을 제대로 이해하지 못한 채 암기만 하는 경우가 많습니다. 특히 마름모의 넓이가 왜 대각선의 곱에 1/2을 곱한 값이 되는지, 또는 왜 밑변과 높이의 곱으로도 넓이를 구할 수 있는지에 대해 질문을 받으면 막연해지는 경우가 적지 않습니다.

이 글에서는 마름모 넓이 공식을 단순 암기가 아닌 ‘도형의 구조’와 ‘기하적 원리’ 관점에서 차근차근 설명합니다. 대각선이 주어졌을 때, 밑변과 높이가 주어졌을 때 각각의 넓이 공식이 어떻게 도출되는지, 그리고 그 공식들이 서로 어떤 관계를 갖는지까지 논리적으로 정리해 드리겠습니다.
마름모 넓이 공식의 기본 개념
마름모는 네 변의 길이가 모두 같은 사각형으로, 평행사변형의 한 종류입니다. 이 사실 하나만 이해해도 마름모 넓이 공식의 절반은 이미 이해한 셈입니다. 평행사변형의 넓이는 기본적으로 ‘밑변 × 높이’로 계산되며, 마름모 역시 예외가 아닙니다. 다만 마름모는 대각선이 서로 수직으로 만나고, 각 대각선이 서로를 이등분한다는 매우 중요한 성질을 갖습니다.

이 대각선의 성질 덕분에 마름모는 삼각형 네 개로 자연스럽게 분할될 수 있고, 이 구조가 대각선 넓이 공식의 핵심 원리가 됩니다. 즉, 마름모 넓이 공식은 새로운 공식이라기보다는 기존 삼각형과 평행사변형 넓이 공식의 응용이라고 볼 수 있습니다.
대각선들의 길이가 주어졌을 때 마름모 넓이 구하는 공식
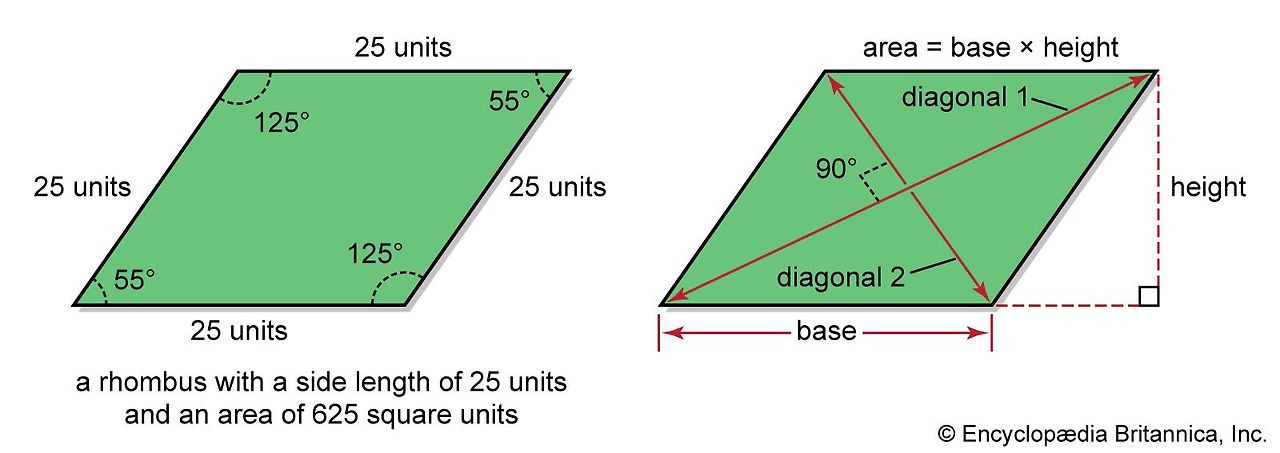
마름모 넓이를 구하는 가장 대표적인 공식은 두 대각선의 길이를 이용하는 방법입니다. 공식은 다음과 같습니다.
- 마름모의 넓이 = $\frac{1}{2} \times d_1 \times d_2$
이 공식이 성립하는 이유를 도형 구조로 살펴보겠습니다. 마름모 ABCD에서 두 대각선이 만나는 점을 O라고 하면, 대각선 AC와 BD는 서로 수직이며 동시에 서로를 정확히 이등분합니다. 이로 인해 마름모는 점 O를 중심으로 서로 합동인 네 개의 직각삼각형으로 나뉩니다. 이때 각각의 삼각형은 밑변이 $\frac{d_1}{2}$, 높이가 $\frac{d_2}{2}$인 직각삼각형입니다. 하나의 삼각형 넓이는 $\frac{1}{2} \times \frac{d_1}{2} \times \frac{d_2}{2}$가 되며, 마름모 전체 넓이는 이 삼각형이 네 개이므로 다음과 같이 계산됩니다.
- $4 \times \frac{1}{2} \times \frac{d_1}{2} \times \frac{d_2}{2} = \frac{1}{2} \times d_1 \times d_2$
이 과정에서 핵심은 ‘대각선이 서로 수직’이라는 성질입니다. 만약 수직이 아니라면 이 유도는 성립하지 않습니다. 따라서 대각선을 이용한 마름모 넓이 공식은 마름모의 고유한 기하적 특징에서 직접적으로 도출된 결과라고 볼 수 있습니다. 예를 들어 대각선의 길이가 각각 9, 8이라면 넓이는 $\frac{1}{2} \times 9 \times 8 = 36$이 됩니다. 단위는 대각선 길이 단위의 제곱이 됩니다.
밑변과 높이가 주어졌을 때 마름모 넓이 구하는 방법
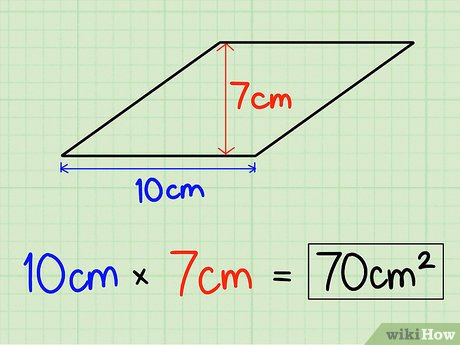

마름모는 평행사변형의 한 종류이므로, 평행사변형의 넓이 공식이 그대로 적용됩니다. 즉, 밑변과 높이가 주어졌다면 넓이는 다음과 같이 계산합니다.
- 마름모의 넓이 = 밑변 × 높이
이 공식은 직관적으로도 이해하기 쉽습니다. 마름모를 기울어진 도형이라고 생각하지 말고, 같은 넓이를 유지한 채 평행 이동하여 직사각형으로 변형한다고 가정하면, 높이는 변하지 않고 밑변 역시 그대로 유지됩니다. 이때 직사각형의 넓이가 밑변과 높이의 곱이므로, 원래의 마름모 넓이 역시 동일하다는 결론에 도달합니다. 이 원리는 평행사변형 넓이 공식의 기본 증명과 동일하며, 마름모라고 해서 별도의 예외가 존재하지 않습니다. 예를 들어 밑변이 15, 높이가 11인 마름모라면 넓이는 165가 됩니다. 이 방식은 대각선 길이를 구하기 어렵고, 높이가 명확히 주어졌을 때 특히 유용합니다.
대각선 공식과 밑변-높이 공식의 관계
대각선을 이용한 공식과 밑변-높이 공식을 서로 다른 공식으로 외우는 경우가 많지만, 실제로는 동일한 넓이를 서로 다른 정보로 표현한 것에 불과합니다. 마름모에서 높이는 ‘밑변에 대한 수직 거리’이며, 이 높이는 대각선과 각의 관계를 통해 계산될 수 있습니다. 다시 말해 대각선의 곱에 1/2를 곱한 값은 결국 밑변과 높이의 곱과 같은 넓이를 만들어냅니다. 이 사실을 이해하면 문제 상황에 따라 어떤 공식을 선택해야 할지 자연스럽게 판단할 수 있습니다. 대각선 길이가 명확히 주어지면 대각선 공식을, 변과 높이가 주어지면 평행사변형 공식을 활용하는 것이 가장 효율적입니다.
결론

마름모 넓이 공식은 단순히 외워야 할 계산식이 아니라, 도형의 구조에서 필연적으로 도출되는 결과입니다. 대각선이 서로 수직으로 만나며 이등분한다는 성질은 마름모를 네 개의 직각삼각형으로 나누게 하고, 이 구조가 $\frac{1}{2} \times d_1 \times d_2$라는 공식을 만들어냅니다. 동시에 마름모가 평행사변형이라는 사실은 밑변과 높이의 곱으로도 넓이를 구할 수 있음을 보장합니다. 이 두 공식은 서로 다른 방식이 아니라 같은 넓이를 서로 다른 관점에서 설명한 결과입니다.



공식을 암기하는 데서 그치지 않고, 왜 그렇게 되는지를 이해한다면 마름모뿐 아니라 다양한 사각형 문제에서도 훨씬 안정적인 사고가 가능해집니다. 기하 문제 해결의 핵심은 결국 도형의 성질을 구조적으로 바라보는 눈이라는 점을 기억하시면 좋겠습니다.


'과학정보' 카테고리의 다른 글
| 감나무 가지치기 시기 | 감나무 전지 방법 (0) | 2026.02.01 |
|---|---|
| 2025년 올해의 과학 사진 - 네이처 선정 최고의 과학 사진 (0) | 2025.12.16 |
| 1kW는 몇마력, 몇 kcal, 1kVA는 몇kW, kW를 마력으로 환산, 단위변환 (0) | 2025.12.12 |
| 1마력은 몇 kW? 마력의 유래와 환산법 (0) | 2025.10.17 |
| 식용버섯 종류 사진과 이름 & 독버섯 (0) | 2025.10.15 |
목차



