원의 면적 구하는 공식, 계산방법
수학에서 가장 기본적이면서도 널리 활용되는 공식 중 하나가 바로 원의 면적을 구하는 공식입니다. 원은 일상 속에서도 흔히 볼 수 있는 도형이지만, 그 성질을 정확히 이해하지 못하면 단순히 눈으로 보이는 크기만으로 면적을 판단하기 어렵습니다. 실제로 원의 넓이는 반지름이나 지름이라는 특정 수치를 기반으로 엄밀하게 계산해야만 구할 수 있습니다.
이번 글에서는 원의 면적 구하는 공식과 구체적인 계산 방법을 단계별로 설명하고, 더 나아가 실생활 속에서 어떻게 응용되는지까지 살펴보겠습니다.
원의 정의와 기초 개념
원을 이해하기 위해서는 먼저 기본적인 정의부터 짚고 넘어가야 합니다.
- 원(circle): 평면 위의 한 정점(중심)에서 일정한 거리에 있는 모든 점의 집합.
- 중심(center): 원의 한가운데 점.
- 반지름(radius, r): 중심에서 원 위의 한 점까지의 거리.
- 지름(diameter, d): 원 위의 두 점을 지나면서 중심을 통과하는 선분. 지름은 반지름의 두 배($d=2r$).
- 원주(circumference): 원의 둘레.
원의 면적은 바로 이 반지름(r)을 이용해 계산할 수 있습니다.
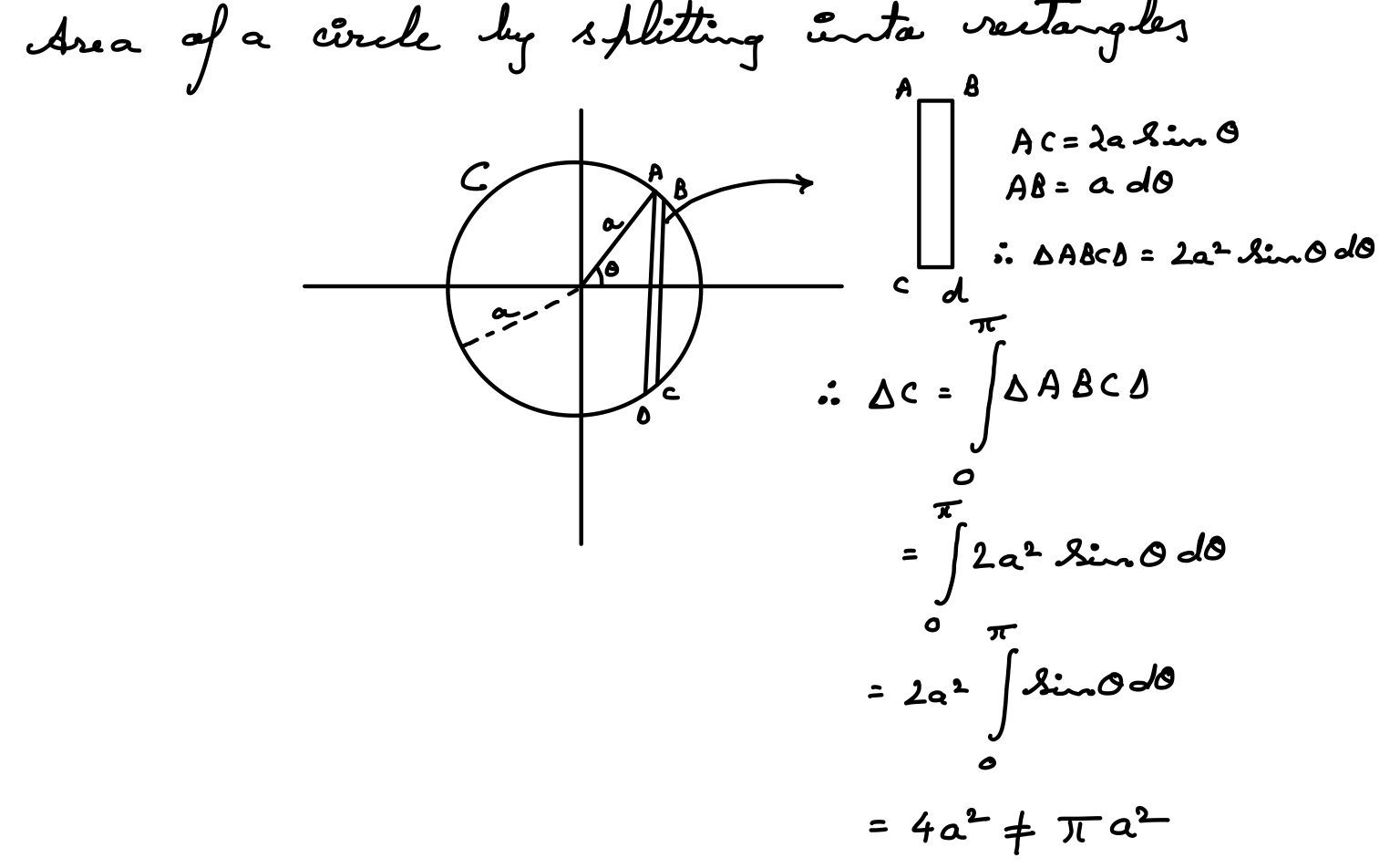
원의 면적 구하는 공식
원의 면적 공식은 다음과 같이 간단히 표현됩니다.
$$
S = \pi r^2
$$
여기서 $S$는 원의 면적, $r$은 반지름, $\pi$(파이)는 원주율을 의미합니다.
- $\pi$는 무리수로, 대략 $3.141592...$의 값을 갖습니다.
- 실제 계산에서는 보통 $\pi \approx 3.14$ 또는 $\pi \approx \frac{22}{7}$로 근사하여 사용합니다.
즉, 원의 면적을 구하려면 반지름의 제곱에 $\pi$를 곱하면 되는 구조입니다.

지름으로 구하는 원의 면적 공식
반지름 대신 지름을 알고 있는 경우도 많습니다. 지름 $d$와 반지름 $r$의 관계는 $d=2r$이므로, 이를 면적 공식에 대입하면 다음과 같습니다.
$$
S = \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{4}
$$
즉, 지름을 알고 있다면 지름의 제곱에 $\pi$를 곱하고 4로 나누면 원의 면적을 구할 수 있습니다.
계산 예시
예시 1: 반지름이 주어진 경우
반지름이 $r=7cm$인 원의 면적을 구해봅시다.
$$
S = \pi r^2 = 3.14 \times 7^2 = 3.14 \times 49 \approx 153.86 , cm^2
$$
예시 2: 지름이 주어진 경우
지름이 $d=10cm$라면?
$$
S = \frac{\pi d^2}{4} = \frac{3.14 \times 100}{4} = \frac{314}{4} \approx 78.5 , cm^2
$$

원의 면적 구하는 공식의 유도 과정
원의 면적 공식은 단순히 외워서 쓰는 것이 아니라, 기하학적으로도 유도할 수 있습니다. 대표적인 방법은 다음과 같습니다.
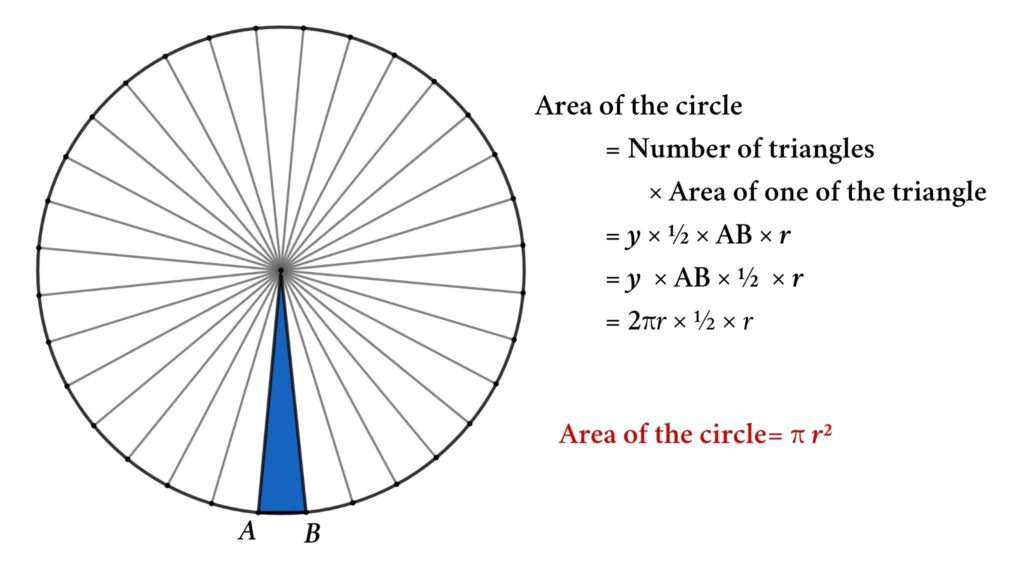
- 원을 잘게 자른 뒤 부채꼴 모양으로 나눔.
- 이를 직사각형에 가까운 형태로 재배열.
- 직사각형의 가로 길이는 원주 절반($\pi r$), 세로 길이는 반지름($r$).
- 따라서 직사각형의 면적은 $\pi r \times r = \pi r^2$.
이 과정을 통해서도 원의 면적 공식을 직관적으로 이해할 수 있습니다.
단위 환산과 주의사항
- 반지름의 단위가 cm라면 면적의 단위는 cm².
- 반지름이 m라면 면적은 m².
- 실생활 계산에서 단위를 혼동하면 큰 오차가 생길 수 있습니다.
예를 들어 반지름이 0.5m인 원과 50cm인 원은 같은 크기이지만, 계산 시 단위를 통일하지 않으면 잘못된 결과가 나올 수 있습니다.
실생활 속 응용
원의 면적 공식은 단순한 수학 문제 풀이에 그치지 않고 다양한 분야에서 활용됩니다.
- 토지 계산: 원형 분수대, 원형 잔디밭의 면적 계산.
- 건축과 인테리어: 원형 기둥의 바닥면적 산출.
- 공학 분야: 원형 기계 부품, 톱니바퀴, 바퀴 면적 계산.
- 일상 생활: 피자의 크기 비교(12인치 vs 16인치 피자).
예를 들어, 12인치 피자(반지름 6인치)의 면적은 약 113in²이고, 16인치 피자(반지름 8인치)의 면적은 약 201in²로, 16인치 피자는 12인치보다 훨씬 넓은 면적을 제공합니다.
다양한 원과 관련된 계산
반원의 면적
원의 절반인 반원의 면적은 다음과 같습니다.
$$
S = \frac{1}{2}\pi r^2
$$
환형(도넛 모양)의 면적
바깥 반지름 $R$, 안쪽 반지름 $r$을 가진 원환형의 면적은
$$
S = \pi R^2 - \pi r^2 = \pi (R^2 - r^2)
$$
원주와의 관계
원의 둘레(원주)는 다음과 같이 구할 수 있습니다.
$$
C = 2\pi r
$$
따라서 면적과 원주 사이에도 긴밀한 관계가 있습니다. 면적은 반지름의 제곱에 비례하고, 원주는 반지름에 비례합니다.
원의 면적 계산 실수 사례
- 반지름과 지름을 혼동하는 경우.
- 단위를 맞추지 않고 계산하는 경우.
- $\pi$를 잘못 근사하는 경우.
이런 실수를 방지하려면 공식과 단위 체계를 정확히 이해해야 합니다.
결론


원의 면적을 구하는 공식은 $S = \pi r^2$로, 단순하지만 깊은 수학적 의미를 담고 있습니다. 이 공식은 기하학적 직관에서 비롯되었으며, 건축, 공학, 생활 속 다양한 영역에서 실질적인 활용 가치를 가집니다. 원의 크기를 평가할 때는 반드시 반지름 또는 지름을 기반으로 계산해야 하며, 단위 관리와 근사값의 정확성이 중요합니다. 단순히 문제 풀이를 위한 공식 암기가 아니라, 실제 상황에서 응용할 수 있도록 이해하는 것이 더 바람직합니다.
'과학정보' 카테고리의 다른 글
| 토란 수확시기, 효능 (0) | 2025.10.11 |
|---|---|
| 상사화 꽃무릇 차이, 개화시기 (0) | 2025.09.26 |
| 12호 태풍 링링 경로예상 현재 위치 - 소멸 (0) | 2025.08.20 |
| 제3호 태풍 문 경로 예상 (0) | 2025.07.02 |
| 소나무 종류 우리나라 곰솔, 조경 잣나무 (0) | 2025.06.22 |
목차



